Egglog

Datalog

• : a subset of Prolog with some key restrictions that make it more predictable and efficient for data processing
• consists of:
  • Facts - Basic statements about data (like “Alice is a parent of Bob”)
  • Rules - Logical implications that derive new facts from existing ones
  • Queries - Questions you ask about the data

% Facts
parent(alice, bob).
parent(bob, charlie).

% Rule
grandparent(X, Z) :- parent(X, Y), parent(Y, Z).

% Query
?- grandparent(alice, charlie).

• :- is read as “if”
• comma is read as “and”

Advanced Features

1. efficient incremental execution
   • recompute results when the underlying data changes, without starting from scratch.
   • When facts are added or removed, the system tracks which derived facts are affected and only recomputes those portions of the analysis.
2. cooperating analyses
   • allows multiple different analyses to share information and mutually refine each other’s results within the same Datalog program.
3. lattice-based reasoning
   • lattice: a partially ordered set in which every pair of elements has a unique supremum and a unique infimum
   • Instead of facts being simply present or absent, they can have values from a partially ordered set where:
     • There’s a “bottom” element (least precise)
     • There’s a “top” element (most precise)
     • Values can be compared and combined using lattice operations (join/meet)

Equality saturation (EqSat)

• : a technique for program optimization that systematically explores equivalent program representations to find the best one

Core concept: EqSat works by

1. representing programs as e-graphs
2. saturating the e-graph by repeatedly applying rewrite rules until no new equalities can be found
3. extracting the best equivalent program according to some cost function

Benefits:

• explores the entire space: traditional optimizers apply transformations sequentially and might get stuck in local minima.
• completeness: given enough time and rules, it will find all equivalent expressions reachable by the rewrite rules.

Applications:

• Compiler optimization
• Query optimization: database systems use it to find optimal query execution plans
• Computer algebra: symbolic math systems use it to simplify expressions
• Hardware synthesis: circuit optimization tools use it to minize gate counts

Example: consider optimizing (x + 1) * (x + 1)

1. saturation discovers:
   • original: (x + 1) * (x + 1)
   • commutativity: (1 + x) * (x + 1)
   • CSE: let t = x + 1 in t * t
   • power: (x + 1)²
2. extraction chooses the cheapest form based on target architecture
   • maybe CSE form if multiplication is expensive

Phase-ordering problem in traditional term rewriting:

• : ~ applies one rule at a time and forgets the original term after each step, so it is sensitive to the ordering of the rewrites
• EqSat fires all the rules in each iteration and keeps both original and rewritten terms in a special data structure called the e-graph

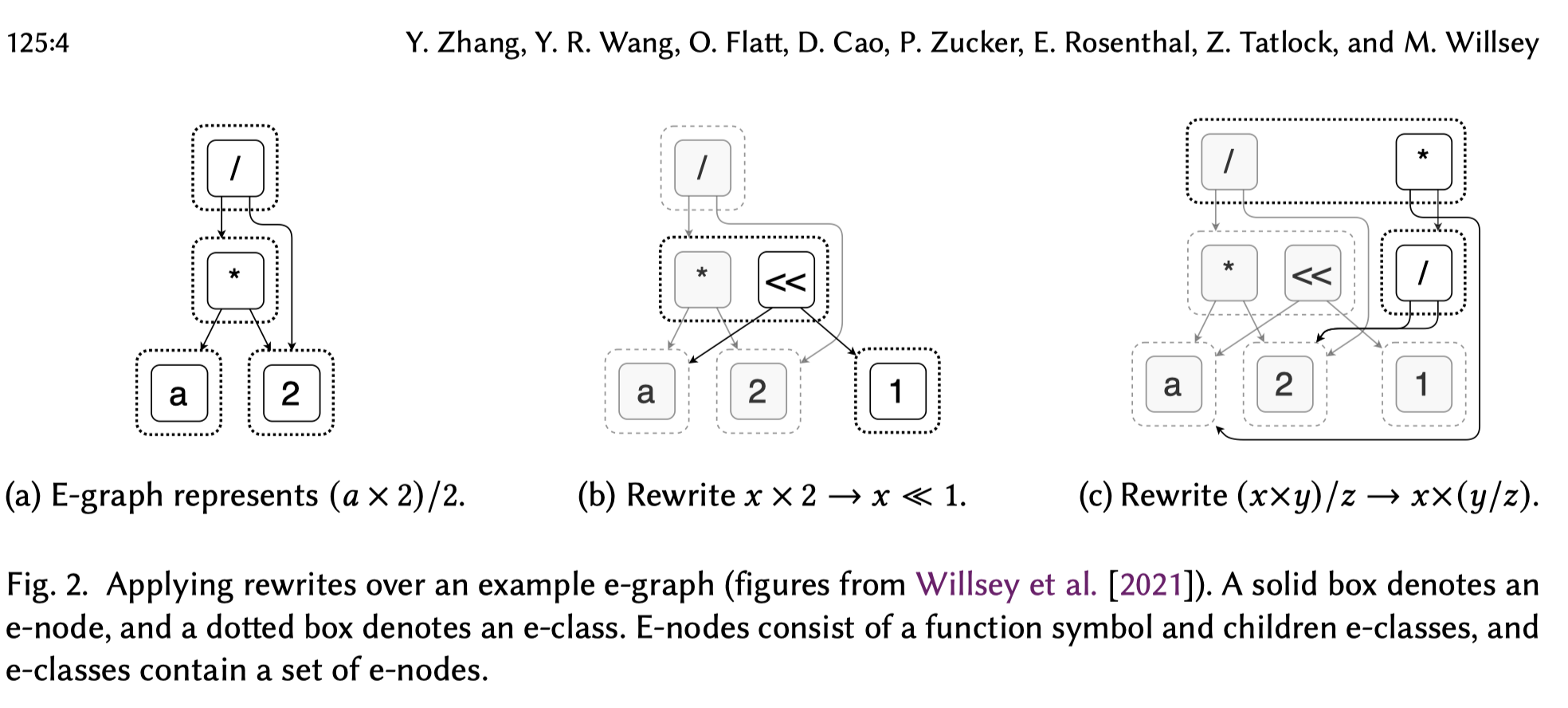
E-graph (equivalence graph)

• : a compact data structure that represents large sets of terms efficiently
• the core innovation that makes equality saturation practical and efficient

Basic structure:

• an e-graph consists of:
  • a set of e-classes
  • each e-classes is a set of equivalent e-nodes
  • an e-node is a function symbol with children e-classes (not e-nodes)
• can compactly represent an exponential number of terms compared to the size of the e-graph
  

Properties:

• congruence closure: If a = b, then f(a) = f(b) is automatically maintained.
• structural sharing: common subexpressions are automatically shared, saving memory
• canonical representation: each equivalence class has a canonical representative, making equality checking O(1)

Operations:

• union: merge two e-classes when you discover they’re equivalent
• find: get the canonical representative of an e-class
• add: insert a new expression

Exponential compression:

• : can represent exponentially many equivalent expressions in polynomial space
• eg: the expression ((a + b) + (c + d)) + ((a + b) + (c + d)) with all reassociations would create thousands of equivalent forms, but the e-graph stores them compactly.

Efficient queries:

• “Are these expressions equivalent?” → O(1) after canonicalization
• “What are all expressions equivalent to X?” → Traverse the e-class

vs. other representations

• ASTs: pick one representation
• DAGs: share identical subexpressions
• Term rewriting: destructively modifies

Applications: e-graphs appears in

• egg: Rust library for e-graphs and equality saturation
• Z3: SMT solver uses e-graphs for theory reasoning
• Cranelift: WebAssembly compiler’s optimization passes
• Herbie:
  • numerical expression optimization:
    • takes a real expression as input
    • returns the most accurate floating-point impolementation it can synthesize
  • core:
    • run equality saturation to explore equivalent programs
    • these programs are mathematically equivalent over the real numbers, but may have different behavior over floating-point numbers.
    • Herbie finds the most accurate among them
• Ruler: Automated rewrite rule inference

Fixpoint reasoning framework

: a computational approach for solving problems where you repeatedly apply rules or transformations until you reach a stable state (the fixpoint) where no further changes occur

• both Datalog and EqSat belong to fixpoint reasoning frameworks

Egglog

• motivation:

  • efficient equational reasoning of EqSat and
  • the rich, composable semantic analyses of Datalog
  • make up for each other’s weaknesses

• : essentially a Datalog engine with two main extensions

  1. a built-in, extensible notion of equality
  2. functions (a functional dependency from its arguments to its output, i.e., output is uniquely determined by the arguments)

• :merge: a function’s :merge expression is used to resolve conflicts in map:

  • conflicts can arise in two ways:
    • 1. the user / a rule calls (set (f x) y) where (f x) is already defined
    • 2. union causes a function’s inputs to become equivalent
  • essentially: user-specified functional dependency repair
    • : the key technical mechanism enabling the synthesis of fixpoint reasoning capabilities of Datalog and EqSat

• implementation:

  • based on a functional database instead of a relational database:
    • ie. each function / relation is backed by a map instead of a set
    • benefit:
      • enable efficient “get-or-default” operation
      • input maps to single output

• Example:

  • : egglog supports classic Datalog programs like reachability written in the natural way. Functions and :merge allow egglog to support Datalog with lattices similar to tools like Flix and Ascent
• 1. Reachability in the classic Datalog style

(relation edge (i64 i64))
(relation path (i64 i64))
(rule ((edge x y))
((path xy)))
(rule ((path x y)(edge y z))
((path x z)))
(edge 1 2)
(edge 2 3)
(edge 3 4)
(run)
(check (path 1 4)）;; succeeds

• 2. Reachability including shortest path length.

(function edge (i64 i64） i64)
(function path (i64 i64) i64 :merge (min old new))
(rule ((= (edge x y) len))
((set (path x y）len)))
(rule ((=(path x y）xy）(=(edge y z)yz))
((set (path x z)(+xy yz))))
(set (edge 1 2) 10)
(set (edge 2 3) 10)
(set (edge 1 3) 30)
(run)
(check (path 1 3)）;;prints "20"

• Example: Unification and EqSat in Egglog
• 1. combining nodes with unification

(sort Node)
(function mk (i64）Node)
(relation edge (Node Node))
(relation path (Node Node))
(rule ((edge x y))
((path x y)))
(rule ((path x y) (edge y z))
((path x z)))
(edge(mk 1）(mk 2))
(edge (mk 2)(mk 3))
(edge (mk 5)(mk 6))
(union (mk 3）(mk 5))
(run)
(check (edge (mk 3）(mk 6)))
(check (path (mk 1）(mk 6)))

2. basic equality saturation

(datatype Math
(Num i64)
(Var String)
(Add Math Math)
(Mu1 Math Math))
;；expr1 =2*(x+ 3)
(define expr1(Mul(Num 2)(Add (Var"x"）(Num 3))))
；；expr2=6+2＊x
(define expr2(Add (Num 6）(Mul (Num 2)(Var "x"))))
(rewrite (Add a b)(Add b a))
(rewrite (Mul a(Add b c))(Add (Mul a b)(Mul a c)))
(rewrite (Add (Num a）(Num b)）(Num(+a b)))
(rewrite (Mul (Num a）(Num b))(Num (* a b)))
(run)
(check (= expr1 expr2))