double category

Definition

• a double category is a category with an extra class of morphisms. Together we have vertical morphism $x \to y$ and horizontal morphism $x \mid\!\!\!\to y$
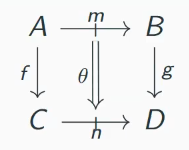
• also, it features a collection of squares, parametrized by two horizontal and two vertical morphisms, with compatible endpoints as follows
  • 
  • the square is also called 2-morphism, or 2-cell
• For vertical and horizontal morphisms we have identities and morphisms
• Difference: laws for vertical morphisms hold up to equality, whereas the laws of horizontal morphisms hold up to a square.
  • this means that we have unitor and associator squares that witness the unitality and associativity of horizontal composition

Different flavors

• strict double category: unitality and associativity of composition holds as an equality
• pseudo double category: composition of horizontal morphisms is only weakly unital and associative
• virtual double category: even weaker

• : $\mathbb{D}$, a pseudo-category internal to categories

  • $\mathbb{D}_0$ = category of objects and arrows
  • $\mathbb{D}_1$ = category of proarrows and cells

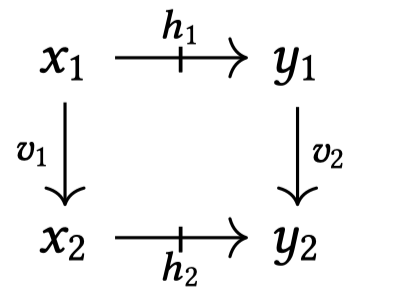
• cells look like

  • 

• $\otimes$ : external composition associative up to coherent isomorphism; external identity functor $y: \mathbb{D}_0 \rightarrow \mathbb{D}_1$

• Examples:

  • sets and spans,
  • sets and relations,
  • categories and profunctors,
  • rings and modules,
  • metric spaces, posets

• Bicategory and 2-category

  • they are double category
    • Any bicategory is a double category without ordinary arrows and cells with trivial external source and target
    • Any 2-category is a double category without proarrows and only cells with trivial internal domain and codomain
  • Likewise any double category has an underlying (2-)category (functional part) and an underlying bicategory (relational part).

• a way to combine or synthesize the theories of functional and relational OLOGs