monoidal category

Idea

: a category equipped with some notion of “tensor product” of its objects
Example: category Vect of vector spaces
The same category can often be made into a monoidal category in more than one way
- informal: Set + cartesian product as tensor product
- informal: Set + disjoint union as tensor product
- informal: Vect + traditional tensor product as tensor product
- informal: Vect + direct sum as tensor product
For any monoidal category $M$ , the operation of tensor product is actually a functor
- $M \times M \otimes M \to M$ .
- it makes $M$ a vertically categorified version of a monoid, which explains the term “monoidal category”.

Definition

A monoidal category is a cateogry $C$ $C$ , equipped with
- a functor: $\otimes: C \times C \to C$ $\otimes : C \times C \to C$
  - from the product category $C \times C$ to $C$
  - called the tensor product
- an object: $1\in C$ $1 \in C$
  - called the unit object or tensor unit
- a natural isomorphism
  - : $a:((-)\otimes(-))\otimes(-)\xrightarrow{\simeq}(-)\otimes((-)\otimes(-))$
  - with component $a_{x,y,z}{:}(x\otimes y)\otimes z\to x\otimes(y\otimes z)$
  - called an associator
- a natural isomorphism
  - $\lambda:(1\otimes(-))\xrightarrow{\simeq}(-)$
  - with component $\lambda_x:1\otimes x\to x$
  - called a left unitor
- a natural isomorphism
  - $\rho:(-)\otimes 1\xrightarrow{\simeq}(-)$
  - with component $\rho_x:x\otimes 1\to x$
  - called a right unitor
such that the following two kinds of diagrams commute, for all objects involved:
- 1. triangle identity
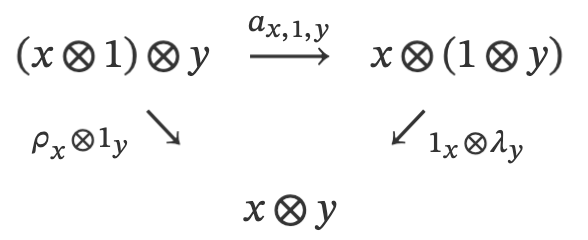
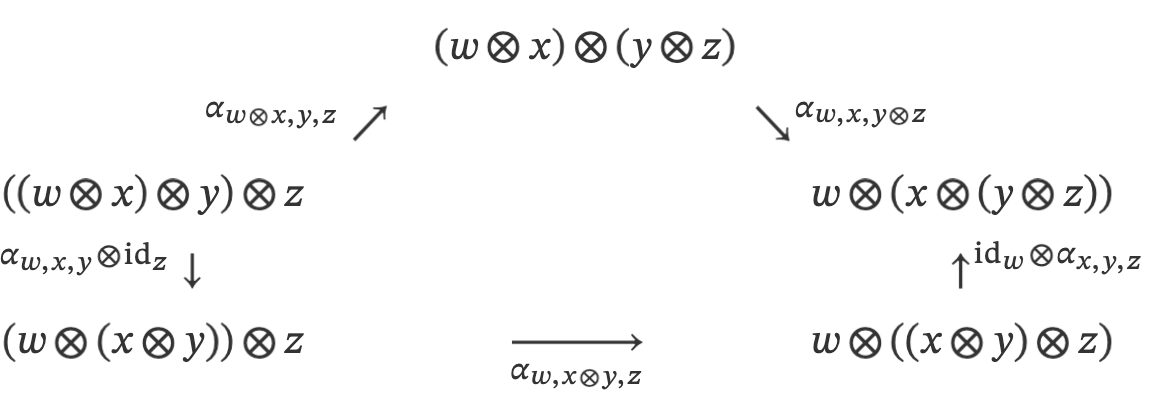
- 1. pentagon identity

Strict monoidal category

A monoidal category is said to be strict if the associator, left unitor and right unitors are all identity morphisms
In this case the pentagon identity and the triangle identities hold automatically.

Properties