Petri net

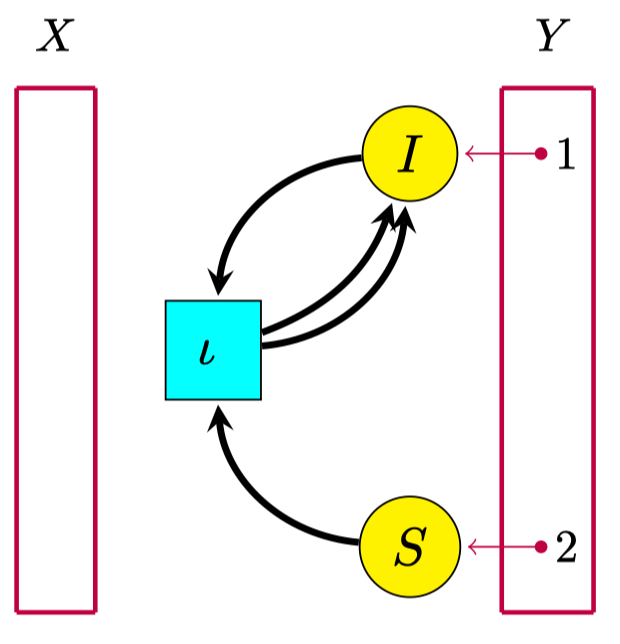
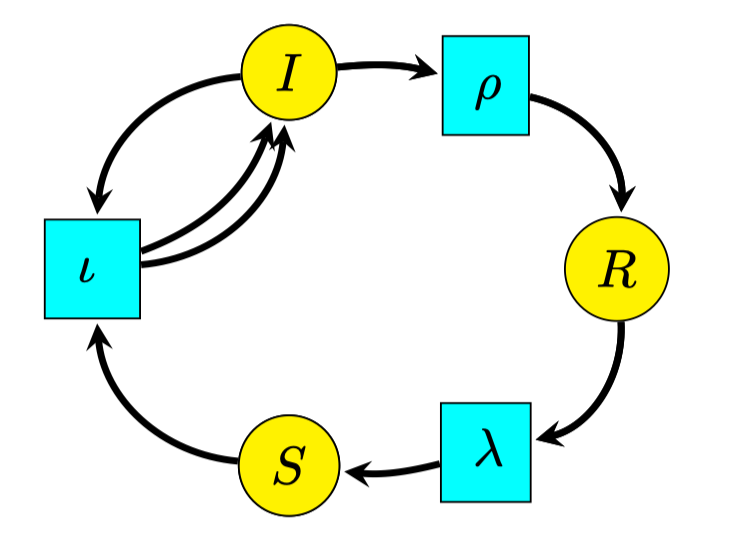
Reaction network $(S, T, s, t)$

• Eg: SIRS infectious disease model
  • $S + I \xrightarrow{\iota} 2I$
  • $I \xrightarrow{\rho} R \xrightarrow{\lambda} S$
  • species:
    • $S$: susceptible
    • $I$: infected
    • $R$: resistant
  • reactions:
    • $\iota$: infection
    • $\rho$: recovery
    • $\lambda$: loss of resistance
• definition:
  • a finite set of species
  • reactions go between “complexes”, which is finite linear combinations of these species with natural number coefficients
• rate constant and rate equation:
  • rate constant: a positive number called can be attached to each reaction
  • rate equation: now a reaction network determines a system of differential equations saying how the concentrations of the species change over time
  • Eg
    • $\frac{dS}{dt} = r_\lambda R-r_\iota SI$
    • $\frac{dI}{dt}=r_\iota SI-r_\rho I$
    • $\frac{dR}{dt} = r_\rho I-r_\lambda R$
  • interesting properties:
    • existence and uniqueness of steady state solutions
• Mathematics definition:
  • consists of:
    • a finite set $S$
      • : elements are called species
    • a finite set $T$
      • : elements are called transitions
    • functions $s, t: T \rightarrow N^S$
      • $N^S$’s elements are called complexes, which is finite linear combinations of these species with natural number coefficients.
      • any transition $\tau \in T$ has a source $s(\tau)$ and a target $t(\tau)$
      • if $s(\tau) = \kappa$ and $t(\tau) = \kappa'$, we write $\tau: \kappa \rightarrow \kappa'$
  • the set of complexes relevant to a given reaction network is
    • : $K = im(s) \cup im(t) \subseteq N^S$
  • graph:
    • a reaction network gives a graph
      • : vertices set of $K$
      • : an edge for each transition $\tau: \kappa \rightarrow \kappa'$
    • it can have multiple edges or self-loops, thus sometimes called:
      • a directed multigraph
      • or a quiver

Petri Net

• bipartite directed graph
  • : 2 kinds of vertices, species and reactions
  • : edges
    • into a reaction, specifying its input
    • out, specifying its output

• Terminology
  • in Petri net literature, species are called “places”, and reactions are called “transitions”
  • so Petri net is sometimes called place-transition net or P/T net
• stochastic Petri net: when each reaction has a rate constant attached
• open Petri net
  • inputs and outputs: species can flow in or out
  • open rate equation: the usual one with extra terms describing inflows and outflows