natural transformation

Idea

• just as a functor is a morphism between categories, a natural transformation is a 2-morphism between functors.

Definition

• Given category $C$ and $D$ and functors $F, G: C \rightarrow D$
• a natural transformation $\alpha: F \Rightarrow G$ between them, denoted
  
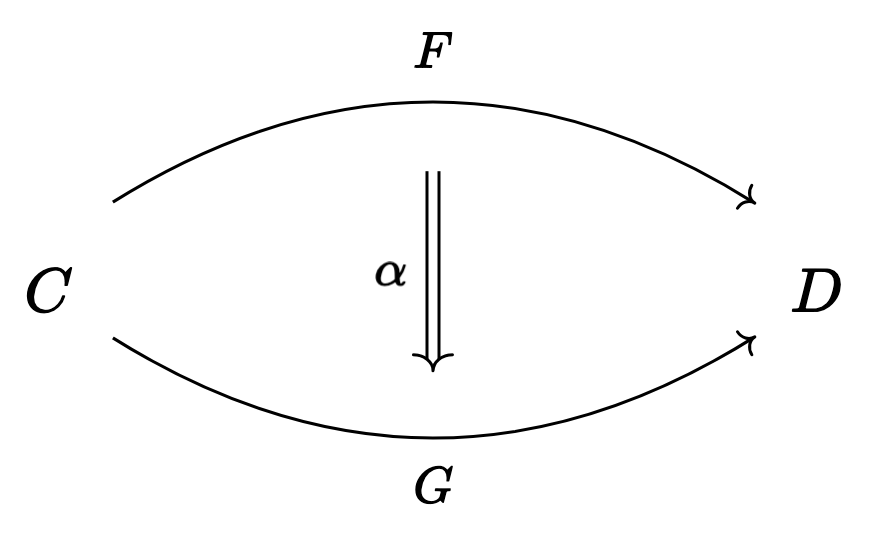
  is an assignment to each object $x$ in $C$ a morphism $\alpha_x: F(x) \rightarrow G(x)$ in $D$, called the component of $\alpha$ at $x$,
• such that the following diagram commutes
  
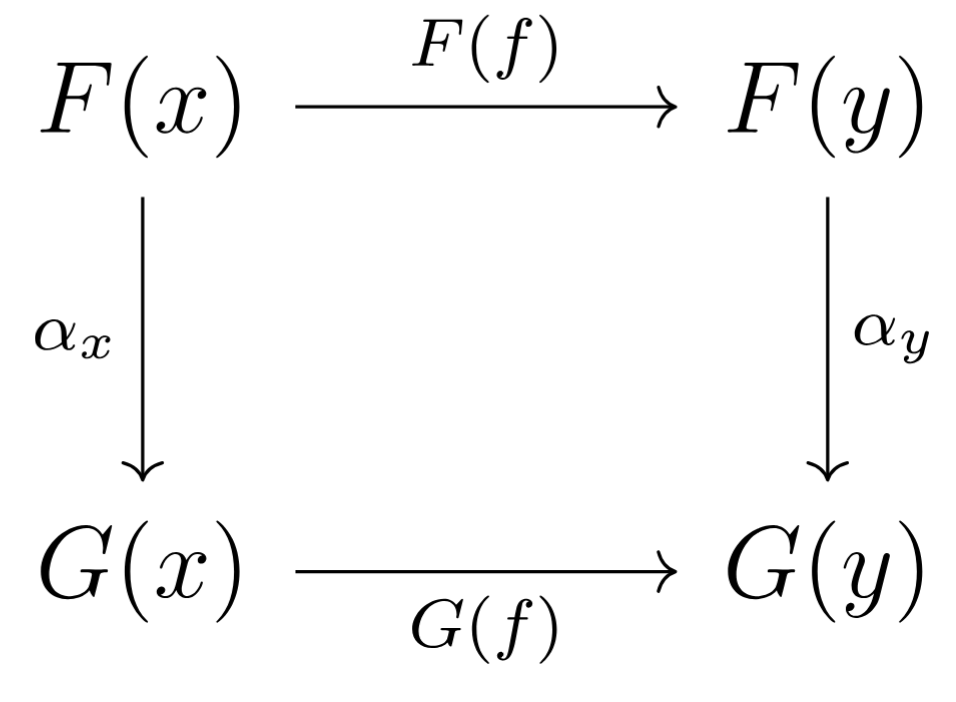
• for $x \xrightarrow{f} y$ in $C$
  • items on top row are given by functor $F$. They are all in $D$
  • bottom row given by functor $G$.

Composition of natural transformation

• Given
  • three functors $F, G, H: C \rightarrow D$,
  • two natural transformations $\alpha: F \Rightarrow G$ and $\beta: G \Rightarrow H$
• composition, $F \Rightarrow H$ , is given obviously.

Alternative definition: in terms of morphism-wise components

• assign every morphism in $C$ a morphism in $D$ such that …
• ultimately equivalent

Quiver links:

• 1