symmetric monoidal category

Idea

• : a monoidal category whose tensor product is as commutative as possible
• There are different degrees to which higher categorical product may be commutative

Definition

• A symmetric monoidal category is a braided monoidal category for which the braiding
  • $B_{x, y}: x \otimes y \to y \otimes x$
  • satisfies the condition: $B_{y, x} \circ B_{x, y} = 1_{x \otimes y}$ for all objects $x, y$
  • Intuitively, this means that switching things twice in the same direction has no effect.
• Expanding the definitions, we can also say a symmetric monoidal category is,
  • (Components) to begin with a category $M$ equipped with:
    • tensor product: a functor $\otimes: M \times M \to M$
    • unit object: an object $1 \in M$
    • associator: natural isomorphism $\alpha_{x, y, z}: (x \otimes y) \otimes z \to x \otimes (y \otimes z)$
    • left unitor: a natural isomorphism $\lambda_x: 1 \otimes x \to x$
    • right unitor: a natural isomorphism $\rho_x: x \otimes 1 \to x$
    • braiding: a natural isomorphism $B_{x, y}: x \otimes y \to y \otimes x$
  • (Laws) We demand that
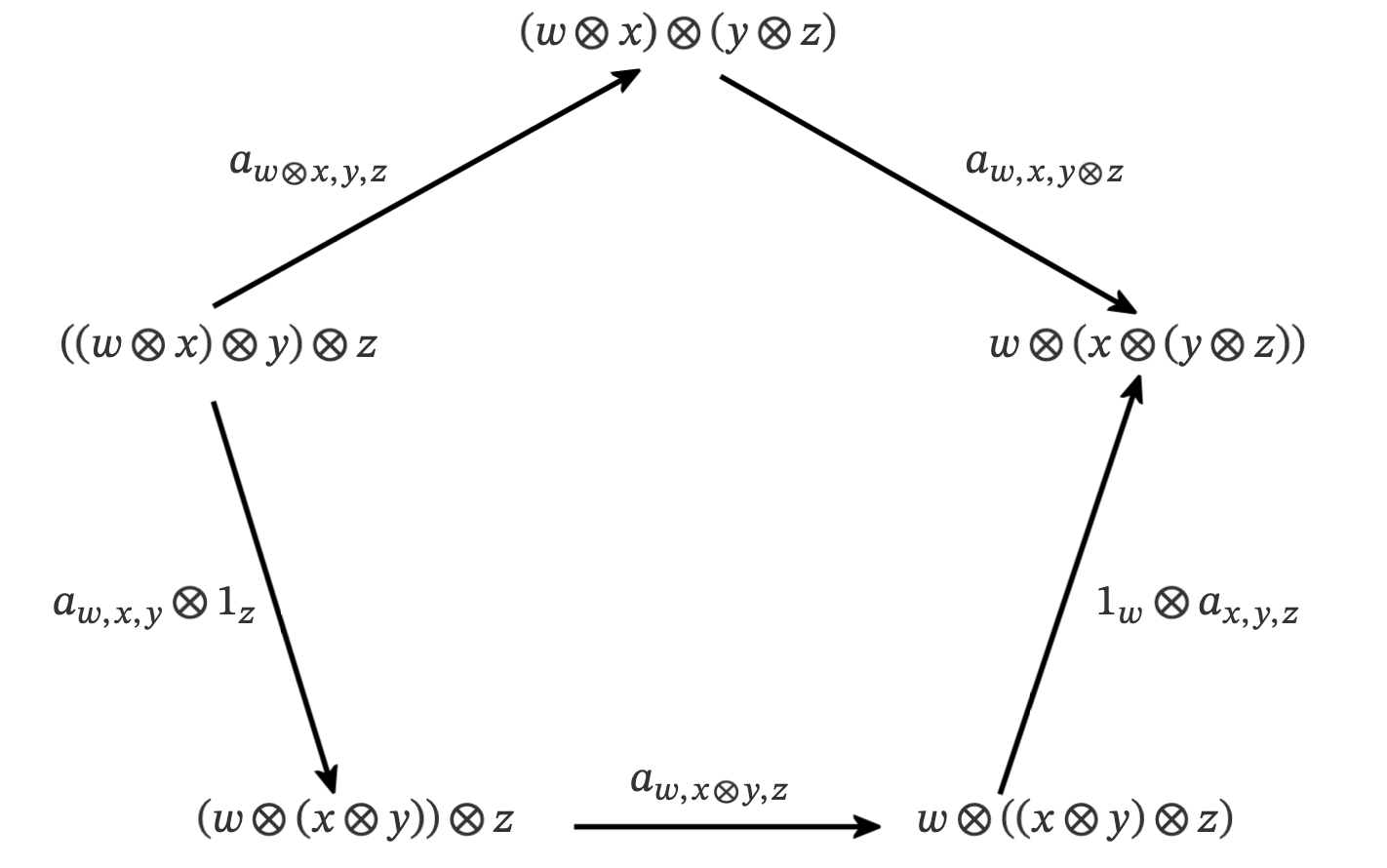
    • the associator obey the pentagon identity, which says this diagram commutes: $1
    • the associator and unitors obey the triangle identity, which says this diagram commutes: $2
    • the braiding and associator obey the first hexagon identity: $3
    • the braiding satisfies: $B_{x, y} \circ B_{y, x} = 1_{x \otimes y}$ for all objects $x, y$

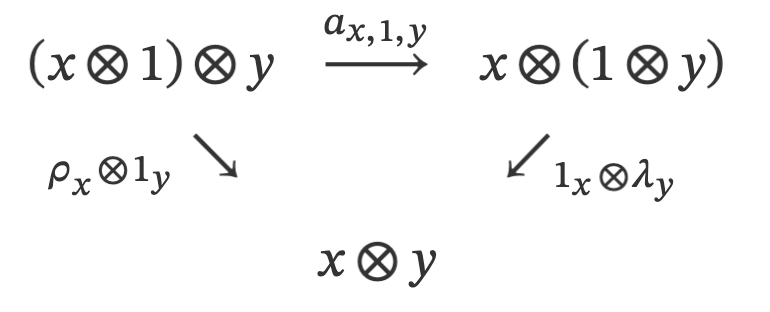
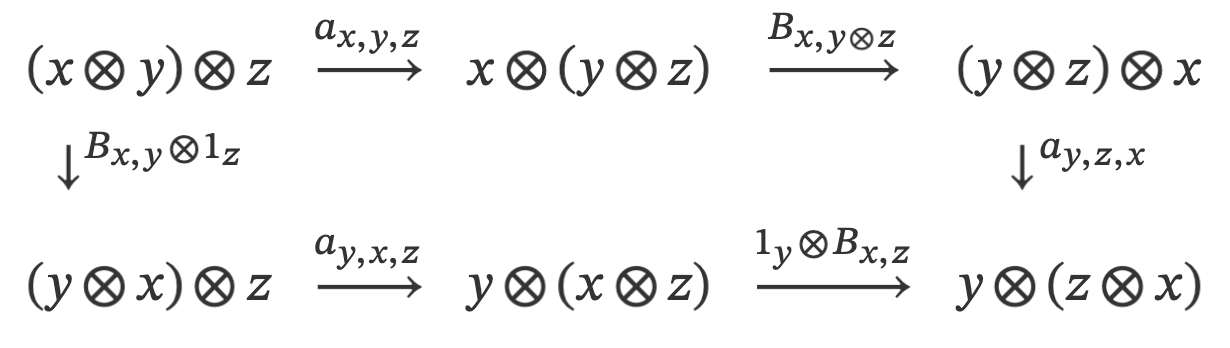
Properties

• …